Octave gyakorlat

Kedves Tanfolyamozók!

Ezen az oldalon találjátok az octave gyakorlathoz készült segédanyagot. Kérlek felkészülten érkezzetek, hogy az előismereteket ne kelljen még egyszer átismételni, és ütemesen tudjunk haladni!

Környezet

A gyakorlat az SCH 103-as gépteremben lesz, így nem kell hozzá saját számítógép, de aki azon szeretne dolgozni (esetleg a gyakorlat után szeretne még kísérletezni) természetesen megteheti. A gyakorlat Octave, illetve Matlab-ban is elvégezhető, a használt parancsok mindkettőben működőképesek.

Amennyiben saját gépen szeretnétek dolgozni, azt a következőképp készítsétek fel:

GNU Octave telepítése: https://wiki.octave.org/Category:Installation
Signal package telepítése (Matlab esetén a signal processing toolbox-ra van szükség, ami néha előre telepítetten érkezik)
- Octave-ben:
  A jelfeldolgozó könyvtárak a Matlab-ban a telepítéssel érkeznek, Octave esetén csomagként érhetők el, és használat előtt be kell tölteni őket. A signal könyvtár a control-ra is támaszkodik, így a megfelelő sorrendben telepítsük őket.
  Írjuk be az Octave parancssorába:
  pkg install -forge control
  pkg install -forge signalAz Octave indulásakor ez nem töltődik be automatikusan, mielőtt jelfeldolgozási függvényeket használnánk, töltsük be a signal comagot:
  pkg load signal
- A signal könyvtárat csomagkezelőből is telepítheted:
  Ubuntu: sudo apt-get install octave-signalArch vagy Manjaro: sudo pacman -S octave-signal
  RPM (OpenSUSE): sudo zypper install octave-forge-signal

Felkészülési segédanyag

Keverés

Az elektromágneses spektrum egy véges erőforrás, így szeretnénk hatékonyan kihasználni.
„Emberi fogyasztásra alkalmas” jeleinket az alapsávban (hangátvitel esetén kb. 20 Hz – 20 kHz között) állítjuk elő, de értelemszerűen ha mindannyian ebben a tartományban forgalmaznánk, akkor nagyon kevés adást tudnánk sugározni, mert mindig csak egymást zavarnánk. Gondoljunk csak arra, amikor mindenki egyszerre beszél az étkezőasztalnál, nagy hangzavar keletkezik, és semmit sem érteni. Épp ezért, az adásainkat szeretnénk az elektromágneses (EM) spektrum különböző tartományiban elhelyezni, így jobban kihasználva azt.

Erre eszközünk a keverés, mellyel jeleinket el tudjuk tolni frekvenciatartományban, vagyis az EM spektrumban. Ez matematikailag két jel összeszorzását jelenti.
A pontos összefüggést a modulációs tétel írja le:

$\cos(\omega_1t) \cdot \cos(\omega_2t) = \frac{1}{2}\cos(\omega_1t+\omega_2t) + \frac{1}{2}\cos(\omega_1t - \omega_2t)$

Ezt a két jelet vivőnek és moduláló (alapsávi) jelnek szokás hívni. A tételben szereplő jelek szinuszosak, de a gyakorlatban a moduláló jelünk tetszőleges lehet. A tétel továbbra is alkalmazható lesz, ugyanis bármilyen jel felbontható szinuszos jelek összegére, és ezek mindegyikére egyenként alkalmazhatjuk a modulációs tételt.

Ha ezt a módszert önmagában alkalmazzuk, azt amplitúdómodulációnak hívjuk (AM). A frekvencia- és fázismodulációkról a tanfolyamon már volt szó, de lentebb átismételjük őket.

Keverés matematikája

Vizsgáljunk csupán egy szinuszjelet, ennél összetettebb jel felfogható több szinusz összegeként, a lentiek igazak erre az esetre is, csak több példányban értelmezve.

Vegyünk egy vektort, ami forog körbe körbe. Vegyük ennek a vektor csücskének az egyik tengelyre vetett árnyékát. A tengelyen a szinusz függvény szerint fog mozogni a pont. Ha ezt a tengelyen mozgó pontot egy ceruzára cseréljük, és egy papírt elkezdünk a mozgására merőlegesen lehúzni egyenletes sebességgel, akkor egy ideális szinuszt fogunk kapni. Bizonyítást lásd: Euler-tétel.

A keverés során semmi mást nem teszünk, mint próbáljuk felvenni a sebességet a jellel. Azaz a vektor továbbra is forog úgy, ahogy forog, viszont a koordináta rendszert elkezdjük forgatni hozzá. Ha ugyan azon irányba, akkor különbségi keverést csinálunk, ha ellentétesbe, akkor összegzőt. (A valóságban persze a kettőt csak együtt tudjuk csinálni. Valós szinusszal keverünk, ami az Euler-tétel miatt két részre bontható, az egyik az egyik, a másik a másik iránynak felel meg.) Ekkor elképzelhető, hogy a kapott szinuszunk lassul vagy gyorsul. Le tudjuk azonos sebesség esetén nullára is lassítani a látszólagos sebességét. Ekkor a szinusz és a koordináta-rendszerünk fázisától függően egy valamilyen álló fázisban látjuk a vektort.

A koordináta-rendszert, amiben ábrázoljuk a lelassított szinuszt, konstellációs diagramnak nevezzük. A vett jel (tfh. szinusz) vektorának a végpontját pedig konstellációs pontnak. Digitális adás esetén szokás a különböző konstellációs térnegyedekhez (vagy ennél is finomabb felbontásokhoz) digitális szimbólumokat rendelni, amiket később (miután rászinkronizált a vevő az adó bitkibocsájtási ütemére) bitfolyamként tud értelmezni egy következő fokozat.

Amplitúdómoduláció (AM)

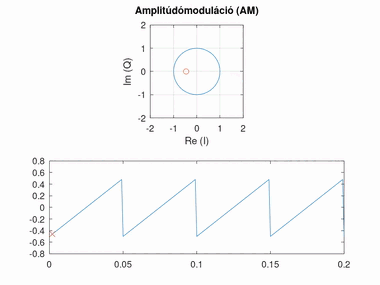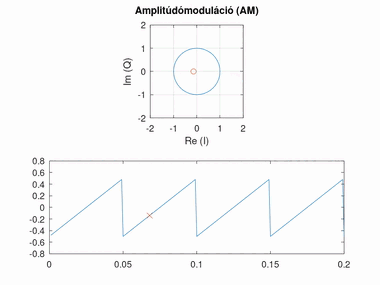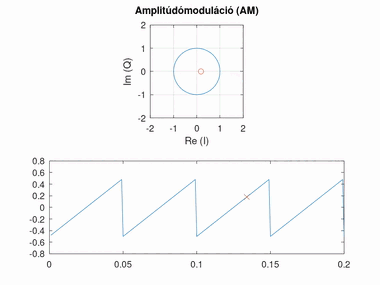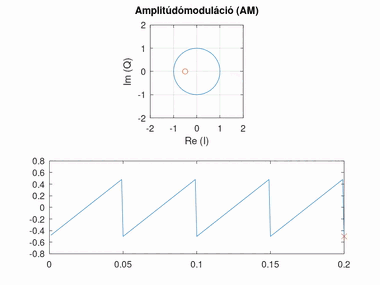
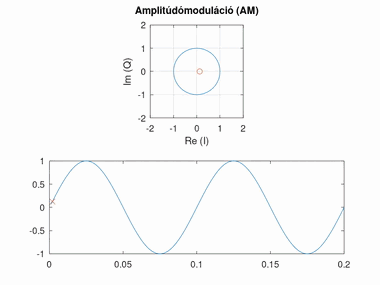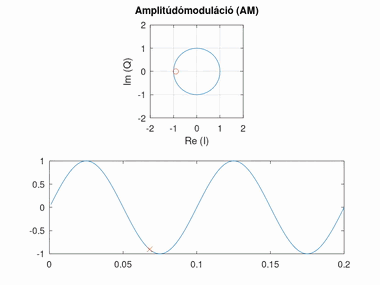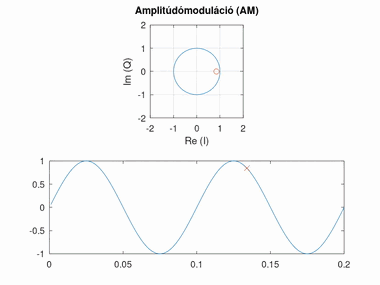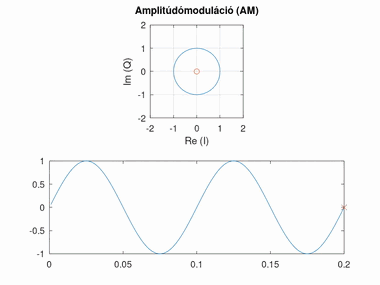
Amplitúdó modulált esetben a konstellációs pont szöge áll, azonban az amplitúdója változik.

Fázismoduláció (PM)

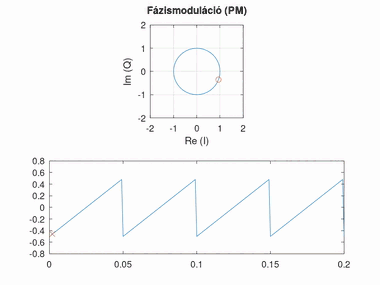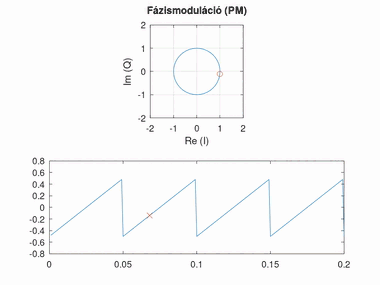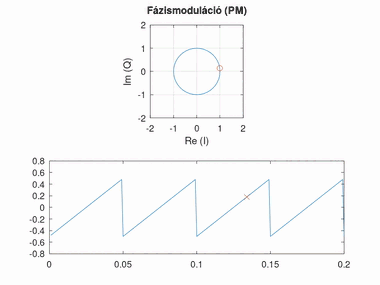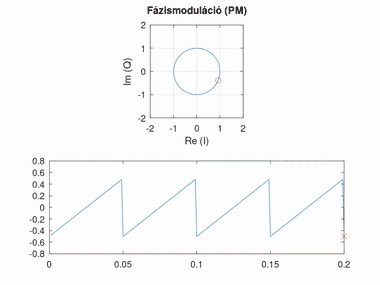
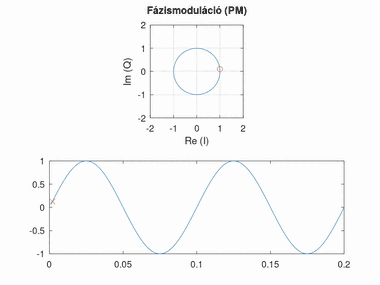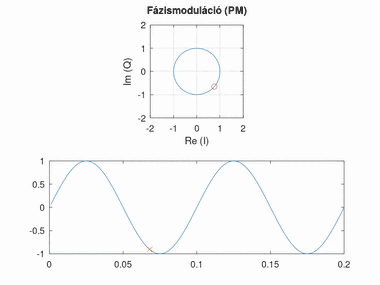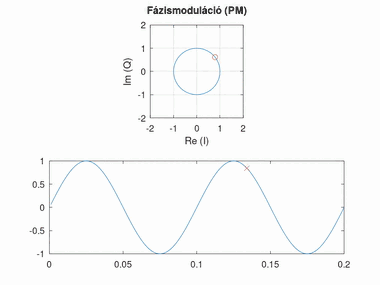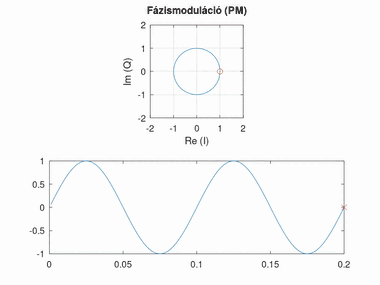
Az alapsávi jel amplitúdóját a modulált jel fázisával reprezentáljuk. A jel 0 feletti értéke a nulla fokhoz képest pozitív, a 0 alatti értéke negatív szöget jelent. Az amplitúdó arányát a szöghöz képest fázislöketnek nevezzük. A fázislöket túl nagy értékénél körbeérhetünk a körön, túl kicsi értéknél viszont nehezen észlelhető a fázisváltozás.

Frekvenciamoduláció (FM)

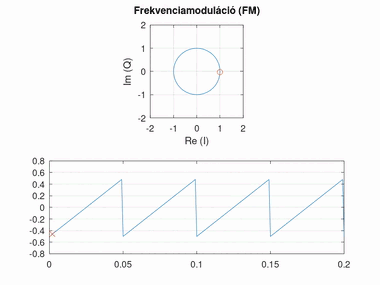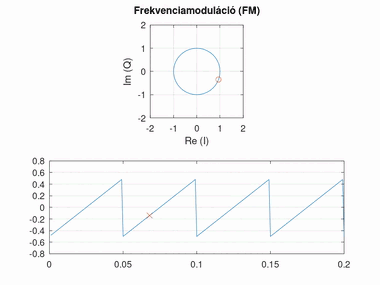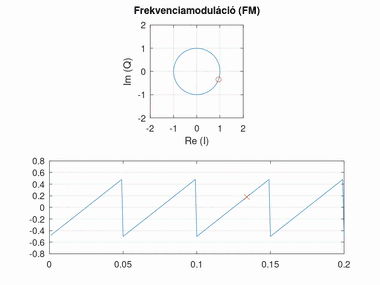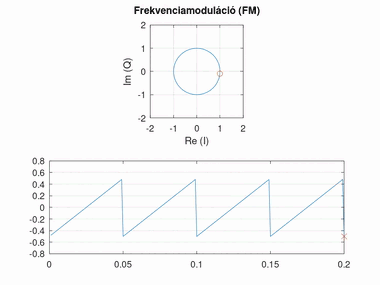
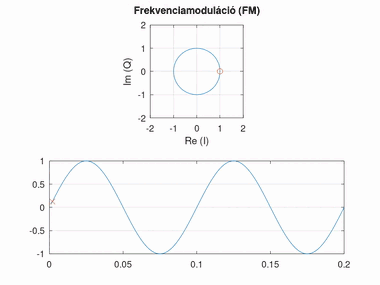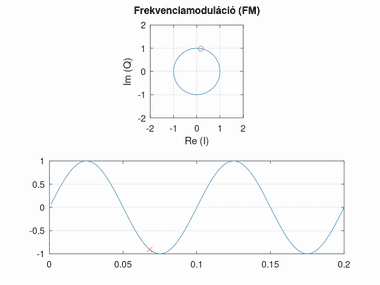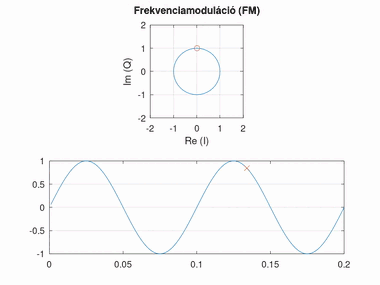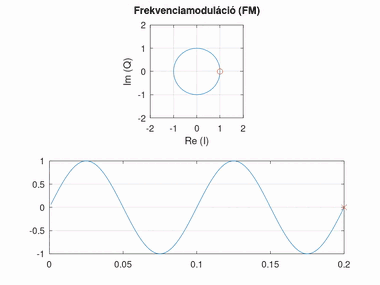
A frekvenciamoduláció nagyban hasonlít a fázismodulációra, azonban itt a fázis változásának mértéke hordozza az információt (tehát a szögsebessége, vagyis a fázis deriváltja). Minél nagyobb a fáziskülönbség két egymást követő pont között, annál nagyobb a moduláló jel amplitúdója. A moduláló jel amplitúdója és a fázisváltozás közti szorzót itt frekvencialöketnek nevezzük.

Kiegészítés: Tükörfrekvencia

Létezik úgynevezett tükörfrekvencia. Ez az a sáv, amit a keverő ugyanarra a frekvenciára kever, mint a hasznos jelet. Vegyünk például egy 100 MHz-es adást, amit 10 MHz-re szeretnénk lekeverni. A modulációs tétel értelmében ezt például úgy érhetjük el, hogy a 100 MHz-es adást megszorozzuk egy 90 MHz-es oszcillátorral (a másik lehetőség egy 110 MHz-es helyi oszcillátor jel lenne), így az 10 MHz-en megjelenik mint különbségi frekvencia. Viszont ekkor a 80 MHz-en lévő spektrumrész is bekeverődik 10 MHz-re a modulációs tétel értelmében. Ezt a bekeverődött, de nem kívánatos frekvenciát hívjuk tükörfrekvenciának. Ezt az eredeti, ide lapolódó spektrumrészt ki kell szűrni a keverés előtt, különben áthallás lesz két adó között.